Mirroring the user’s experience, the implementation of brain2print has two stages. First, the brainchop AI models are used to segment a raw MRI scan (Fig. 2a) into brain regions (2b). The second step converts the segmented voxels into a triangulated mesh (2c). The AI models of the first stage leverage WebGL via TensorFlowJS that harnesses the user’s massively parallel graphics card. In contrast, the second voxel-to-mesh stage leverages the user’s central processing unit (CPU). While we have previously described the brainchop models8, the high performance voxel-to-mesh operations are new and therefore we describe them in more detail here. These new voxel-to-mesh features have been added to our niimath9 project, while we also provide access to slower but more precise functions via a plugin to the itk-wasm project10. Both these projects compile proven tools in the C language to WebAssembly (for web pages, as here).
NiiVue (https://github.com/niivue/niivue) is used to load and display images. This ensures drag and drop support for common interchange formats including DICOM, NRRD and NIfTI. The DICOM format and file organization is particularly complicated, and therefore NiiVue is not able to read all variations of this format. In cases where users are unable to import DICOM images directly, they can use dcm2niix to import images11. In addition, it can also read the native proprietary voxel-based image formats of many popular tools, including MRtrix12 (MIF extension), AFNI13 (BRIK), FreeSurfer4, and DSI-Studio14 (SRC). As seen in Fig. 1, NiiVue allows the user to interactively inspect the voxel-based image, the AI-aided segmentation as well as the resulting triangulated mesh. This allows the user to fine-tune the mesh prior to the time consuming mesh printing process. Finally, NiiVue supports various export formats for the resulting triangulated mesh, specifically STL, WaveFront OBJ and MZ3.
Trade offs in mesh creation
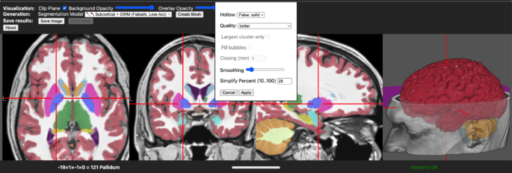
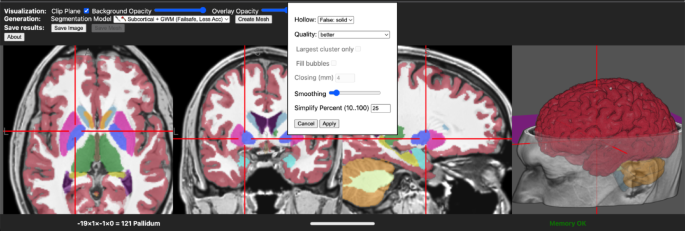
Converting voxel-based data into a mesh involves key decisions that influence the shape of the final surface. As shown in Fig. 2, directly generating a mesh from binary segmentation (2B) often results in a jagged surface (2 C), which may require smoothing for better appearance and usability (2D). Large, complex volumes can also create oversized mesh files, necessitating simplification to reduce file size (2E).
The optimal mesh topology depends on the intended use case15. Elongated triangles are considered ideal for triangle simplification algorithms focused on minimizing geometric error but are unsuitable for applications like finite element simulations16. Similarly, faster methods may introduce subtle defects, such as holes or self-intersecting triangles. While modern 3D printing tools generally tolerate these issues, they can pose challenges in other contexts. To accommodate diverse needs and equipment, our approach provides two pipeline options: one for faster processing that minimizes geometric error and another that prioritizes defect prevention and produces more uniformly shaped and sized triangles.
For 3D printing, additional considerations arise. Unlike meshes for computer visualization, printed meshes are typically hollow to minimize material usage, increasing complexity. The surface thickness must align with the printing material, and hollow meshes require escape holes for filler material removal.
Fast mesh creation
Our fast pipeline is optimized for rapid mesh generation, achieving processing times of mere seconds, even on outdated, battery-powered devices—a claim substantiated in the results section. The development for this pipeline prioritized performance, with extensive testing of several variants of Sven Forstmann’s implementation of mesh simplification using quadric error metrics17. which focuses on minimizing geometric error.
We found that WebAssembly methods are faster than pure JavaScript methods if binary data transfer is used, but that WebAssembly faces a huge penalty if triangulated meshes are passed as ASCII text (the WaveFront OBJ format). This can be seen with our live demo web page (https://neurolabusc.github.io/simplifyjs/) where one can selectively choose the simplification method. Specifically, we found simplifying the ‘brain’ mesh from 327,678 to 81,920 triangles (removing 75%) required 841ms with the fastest pure JavaScript method (‘niivue’), 1118ms for web assembly with text transfer (WASM) and 256ms when combining web assembly and binary transfer (WASMmz3). We also determined that Sven Forstmann’s original C + + implementation could be optimized by using pure C code that focused on pre-allocating arrays (presumably, there is a penalty for growing arrays in WebAssembly). This finding is demonstrated by our live demo (https://neurolabusc.github.io/niivue-simplify/) where reducing the number of triangles to 25% for the lh.mz3 mesh required 277ms for the C + + code and 209ms for the pure C implementation. Based on this survey, the fastest C code compiled to WebAssembly is included for brain2print. The subsequent evaluation builds on this optimized code.
Precise mesh creation
Our fast method produces meshes suitable for modern 3D printers but makes trade-offs that may not be ideal for all use cases. Specifically, it often generates anisotropic triangles to preserve mesh shape while minimizing complexity. Additionally, this method can introduce minor defects, such as small holes (compromising watertightness) and self-intersecting triangles. While these defects can often be repaired with offline tools, minimizing their occurrence during mesh creation is preferable for some use cases.
To address this, we provide a slower but more accurate mesh creation pipeline based on the “cuberille” method for polygonization of implicit surfaces18 as implemented in the ITK-wasm repository10. This approach prioritizes the creation of defect-free meshes with uniformly sized and nearly equilateral triangles. Since the method has been described in detail elsewhere and is not focused on performance optimization, we do not evaluate its runtime in the results section.